Ciri-ciri Prism Heptagonal dan Cara Menghitung Jilid
A prisma heptagonal adalah tokoh geometrik yang, seperti namanya, melibatkan dua definisi geometri iaitu: prisma dan heptagon.
"Prisma" adalah angka geometri yang dibatasi oleh dua pangkalan yang sama dan poligon selari dan muka sampingannya adalah parallelograms.
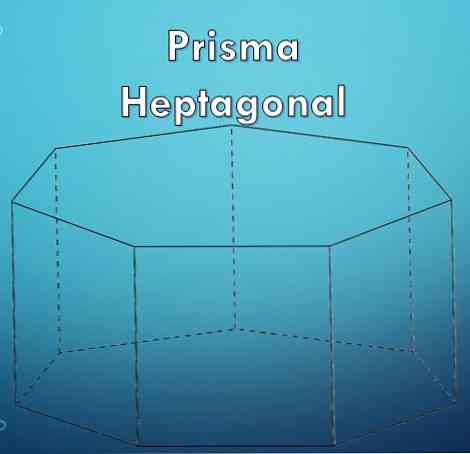
"Heptagon" adalah poligon yang dibentuk oleh tujuh (7) pihak. Oleh kerana heptagon adalah poligon, mungkin ia adalah biasa atau tidak teratur.
Poligon dikatakan tetap jika semua pihak memiliki panjang yang sama dan sudut dalamannya mengukur sama, mereka juga dipanggil poligon sama-sama; jika tidak dikatakan bahawa poligon tidak teratur.

Ciri-ciri Prism Heptagonal
Berikut adalah ciri-ciri tertentu yang mempunyai prisma heptagonal seperti: pembinaannya, sifat asasnya, kawasan semua muka dan jumlahnya.
1- Pembinaan
Untuk membina prisma heptagonal dua heptagons diperlukan, yang akan menjadi asasnya dan tujuh paralelogram, satu pada setiap sisi heptagon.
Mulailah dengan melukis heptagon, kemudian lukis tujuh garisan menegak, panjang yang sama, yang datang dari setiap simpangnya.
Akhir sekali, heptagon lain ditarik supaya titik-titiknya bertepatan dengan akhir garisan-garis yang dilukis dalam langkah sebelumnya.
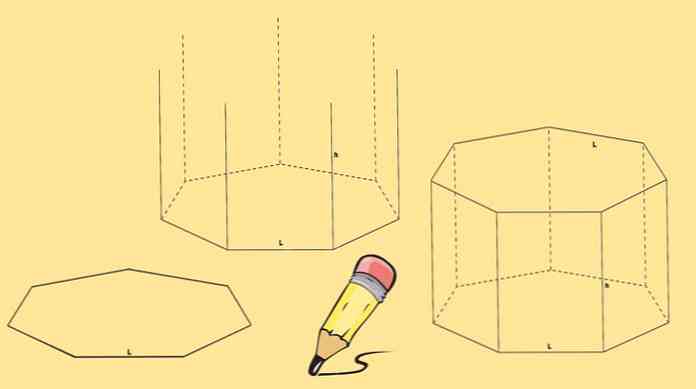
Prisma heptagon yang diletakkan di atas dipanggil prisma heptagonal lurus. Tetapi anda juga boleh mempunyai prisma heptagonal serong seperti yang ada dalam angka berikut.

2- Sifat asasnya
Sejak asas adalah heptagons, ini memenuhi jumlah pepenjuru adalah D = nx (n-3) / 2, di mana "n" adalah bilangan sisi poligon; dalam kes ini mesti D = 7 × 4/2 = 14.
Kita juga boleh melihat bahawa jumlah sudut dalaman mana-mana heptagon (biasa atau tidak teratur) adalah sama dengan 900º. Ini boleh disahkan oleh imej berikut.
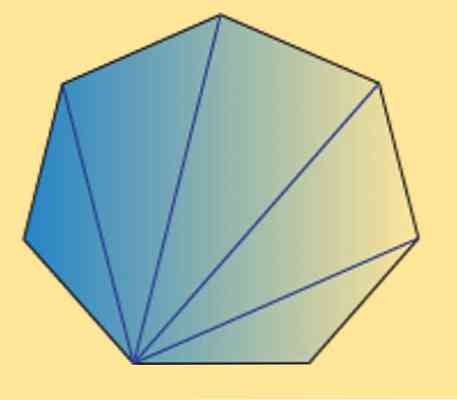
Seperti yang dapat anda lihat, terdapat 5 segitiga dalaman, dan menggunakan jumlah sudut dalaman segi tiga adalah sama dengan 180º, dapat diperoleh hasil yang diinginkan.
3- Kawasan diperlukan untuk membina Prisma Heptagonal
Sebagai pangkalan adalah heptagons dan kedua-dua pihak adalah selari tujuh, kawasan yang diperlukan untuk membina sebuah prisma heksagon adalah sama dengan + 2xH 7XP mana "H" adalah kawasan setiap heptagon dan "P" keluasan setiap selari.
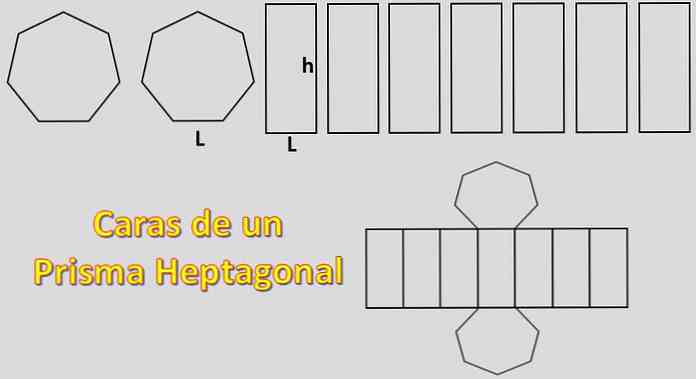
Dalam kes ini, kawasan heptagon biasa akan dikira. Untuk ini, penting untuk mengetahui definisi apothema.
Apotem adalah garis tegak lurus yang keluar dari pusat poligon biasa ke titik tengah mana-mana bahagiannya.
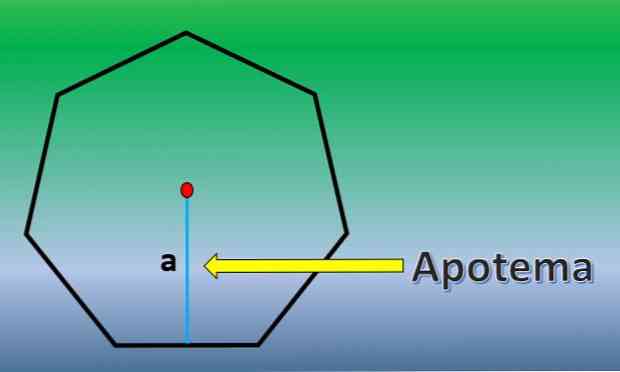
kawasan apotema pernah dikenali perlu heptagon adalah H = 7xLxa / 2, di mana "L" adalah panjang setiap sisi dan "a" panjang apotema.
Kawasan segi empat selari adalah mudah untuk mengira, ditakrifkan sebagai P = LxH, di mana "L" adalah heptagon sisi sama panjang dan "h" adalah kemuncak prisma.
Kesimpulannya, jumlah yang diperlukan untuk membina bahan prisma heptagonal (secara tetap) adalah 7xLxa + 7xLxh, iaitu 7XL (a h +).
4- Volume
Sebaik sahaja kawasan asas dan ketinggian prisma diketahui, isipadu ditakrifkan sebagai (kawasan asas) x (ketinggian).
Dalam kes prisma heptagonal (dengan asas tetap) ia mempunyai jumlahnya ialah V = 7xLxaxh / 2; juga boleh ditulis sebagai V = Pxaxh / 2, di mana "P" adalah perimeter heptagon biasa.
Rujukan
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematik: pendekatan penyelesaian masalah untuk guru pendidikan asas. López Mateos Editores.
- Fregoso, R. S., & Carrera, S. A. (2005). Matematik 3. Progresial Editorial.
- Gallardo, G., & Pilar, P. M. (2005). Matematik 6. Progresial Editorial.
- Gutiérrez, C. T., & Cisneros, M. P. (2005). Kursus Matematik Ketiga. Progresial Editorial.
- Kinsey, L., & Moore, T. E. (2006). Simetri, Bentuk dan Ruang: Pengenalan kepada Matematik Melalui Geometri (digambarkan, dicetak semula ed). Sains & Media Perniagaan Springer.
- Mitchell, C. (1999). Reka Bentuk Talian Matematik yang mempesonakan (Illustrated ed.). Inc Scholastic.
- R., M. P. (2005). Saya menarik 6º. Progresial Editorial.


